Function Viewer 1.0

This is a simple function viewer program (using the Gtk+ graphics library) to showcase my Function Parser library.

Notable features:

The functions are drawn as soon as there's a valid function written in a function field. No clicking "ok", not even pressing enter: Just write and the the program will draw the function as soon as it's anything valid.
Write any amount of functions. They will all be drawn using a selectable color.
Subsequent functions can call any previous function (as showcased in the screenshot below).
Turn drawing any function off or on.
Zoom and scroll the view in real time using the mouse. No entering cumbersome limit values in textfields, just click&drag the viewing area. (Left mouse button for zooming, right mouse button for scrolling.)
The aspect ratio (y axis zoom) can also be controlled (ctrl + left mouse button).

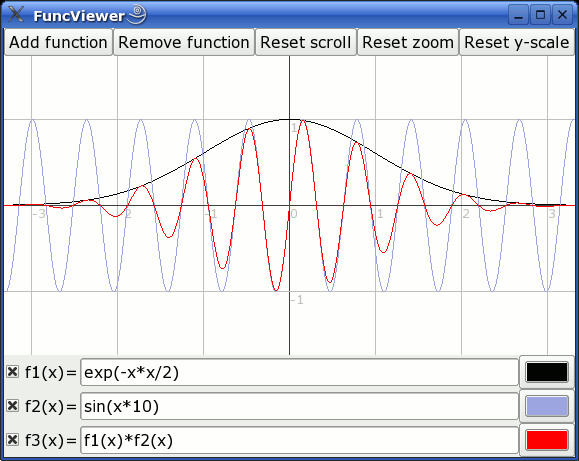
Example screenshot:

Download

This program is distributed under the GPL license.

Windows

Download the full Windows binary distribution (2.7MB). This contains the executable and the required GTK DLL files (they will not be installed in your system, but will just remain in the same folder as the executable).

Simply extract the contents of the zip file into some folder, and run the executable to run the program. No installation needed. When you want to remove the program, simply remove the entire folder.

Download the executable only (46kB). If the GTK+-2.x Windows runtime libraries are already installed in your system (eg. because you have installed the Gimp), chances are that the exe alone will work all by itself.

Linux/Unix

Download a Linux binary, if you don't want to hassle with compiling the program. The program requires the GTK+-2.x runtime library to be installed in the system (the binary was compiled against GTK+-2.6.4). In case the program doesn't work you'll have to compile it for your system from the sources given below.

Download the Unix source code. A simple "make" should compile it in most Linux systems. Requires the GTK+-2.x devel libraries to be installed in the system.

Function syntax

The functions understood by the program are very similar to math expressions in the C language.

Arithmetic float expressions can be created from float literals, variables or functions using the following operators in this order of precedence:

`()`	expressions in parentheses first
`A^B`	exponentiation (A raised to the power B)
`-A`	unary minus
`!A`	unary logical not (result is 1 if int(A) is 0, else 0)
`A*B A/B A%B`	multiplication, division and modulo
`A+B A-B`	addition and subtraction
`A=B A!=B A<B A<=B A>B A>=B`	comparison between A and B (result is either 0 or 1)
`A&B`	result is 1 if int(A) and int(B) differ from 0, else 0
`A\|B`	result is 1 if int(A) or int(B) differ from 0, else 0

Since the unary minus has higher precedence than any other operator, for example the following expression is valid: x*-y

The class supports these functions:

abs(A) : Absolute value of A. If A is negative, returns -A otherwise returns A.
acos(A) : Arc-cosine of A. Returns the angle, measured in radians, whose cosine is A.
acosh(A) : Same as acos() but for hyperbolic cosine.
asin(A) : Arc-sine of A. Returns the angle, measured in radians, whose sine is A.
asinh(A) : Same as asin() but for hyperbolic sine.
atan(A) : Arc-tangent of A. Returns the angle, measured in radians, whose tangent is (A).
atan2(A,B) : Arc-tangent of A/B. The two main differences to atan() is that it will return the right angle depending on the signs of A and B (atan() can only return values betwen -pi/2 and pi/2), and that the return value of pi/2 and -pi/2 are possible.
atanh(A) : Same as atan() but for hyperbolic tangent.
ceil(A) : Ceiling of A. Returns the smallest integer greater than A. Rounds up to the next higher integer.
cos(A) : Cosine of A. Returns the cosine of the angle A, where A is measured in radians.
cosh(A) : Same as cos() but for hyperbolic cosine.
cot(A) : Cotangent of A (equivalent to 1/tan(A)).
csc(A) : Cosecant of A (equivalent to 1/sin(A)).
exp(A) : Exponential of A. Returns the value of e raised to the power A where e is the base of the natural logarithm, i.e. the non-repeating value approximately equal to 2.71828182846.
floor(A) : Floor of A. Returns the largest integer less than A. Rounds down to the next lower integer.
if(A,B,C) : If int(A) differs from 0, the return value of this function is B, else C.
int(A) : Rounds A to the closest integer. 0.5 is rounded to 1.
log(A) : Natural (base e) logarithm of A.
log10(A) : Base 10 logarithm of A.
max(A,B) : If A>B, the result is A, else B.
min(A,B) : If A<B, the result is A, else B.
sec(A) : Secant of A (equivalent to 1/cos(A)).
sin(A) : Sine of A. Returns the sine of the angle A, where A is measured in radians.
sinh(A) : Same as sin() but for hyperbolic sine.
sqrt(A) : Square root of A. Returns the value whose square is A.
tan(A) : Tangent of A. Returns the tangent of the angle A, where A is measured in radians.
tanh(A) : Same as tan() but for hyperbolic tangent.

Additionally, any function name with a number smaller than the current one can be used in the current function. For example, f2(x) can call f1 eg. like this: "2*f1(x*5)"

The constant "pi" is supported.

Examples of function string understood by the program:

1+2
x-1
-sin(pi*sqrt(x^2))
exp(-x*x)*sin(x*10)