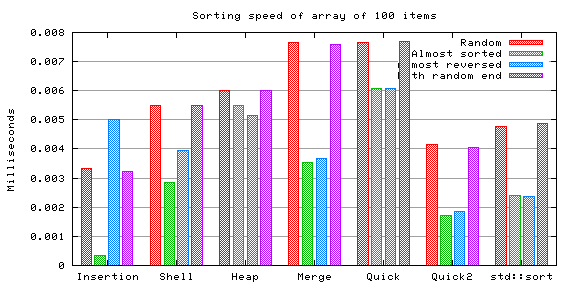
The test was performed by generating an array of 100, 5000, 100000 and 1 million random integers. The values of these integers were between 0 and 10 times the size of the array (thus there's minimal repetition). The different distributions were explained in the main page.
Integers are very fast to compare and to copy, so this testcase measures what could perhaps be called "raw sorting speed".
Each bar in the charts expresses the time taken by the sorting algorithm, in average, to sort the array once, in milliseconds. (The time used to generate the contents of the array were substracted from the total time, as described in the main page.) Thus lower bars are better.

In this case the "random end" testcase was basically identical to the totally random testcase because the 256 last items of the array were random, and in this case the entire array was thus random. This is the reason why both bars are (approximately) equal for all algorithms.
Insertion sort, an O(n2) algorithm, compares very well with the "faster" algorithms when the array is small enough, like this one. As seen in the chart, when the array is almost sorted, insertion sort is tremendously faster than anything else. It was not tested with larger arrays, though, because it becomes really slow very fast as the array size increases.
| Random | Almost sortd | Almost rev. | Random end | |||||
|---|---|---|---|---|---|---|---|---|
| Alg. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. |
| Insert. | 2567 | 2670 | 418 | 517 | 4704 | 4827 | 2567 | 2670 |
| Shell | 767 | 1076 | 463 | 747 | 731 | 1092 | 767 | 1076 |
| Heap | 1027 | 1743 | 1069 | 1882 | 957 | 1558 | 1027 | 1743 |
| Merge | 558 | 800 | 470 | 800 | 424 | 800 | 558 | 800 |
| Quick | 1062 | 475 | 2809 | 241 | 2053 | 335 | 1062 | 475 |
| Quick2 | 783 | 724 | 691 | 393 | 599 | 487 | 783 | 724 |
The effect of insertion sort being an O(n2) algorithm can be seen in the amount of comparisons and assignments it performs even for such a small array. The reason why it manages to be faster than most of the others in this case is that its inner loop is extremely simple and thus has almost no "overhead". Naturally it rapidly loses this advantage when the array grows any larger than this.
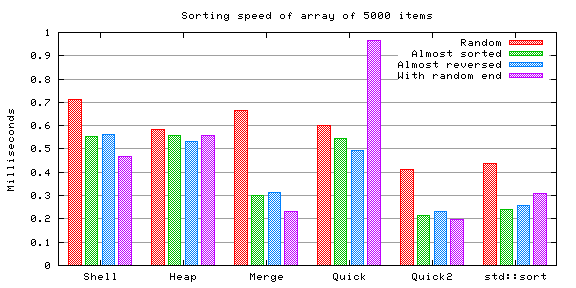
The "random end" testcase starts to show its pathological nature in the vanilla quicksort case already with 5000 integers.
| Random | Almost sortd | Almost rev. | Random end | |||||
|---|---|---|---|---|---|---|---|---|
| Alg. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. |
| Shell | 101319 | 136506 | 76299 | 109854 | 81419 | 118739 | 67994 | 101395 |
| Heap | 107688 | 171318 | 109588 | 177608 | 103758 | 161272 | 111986 | 181244 |
| Merge | 56823 | 70000 | 51726 | 70000 | 51449 | 70000 | 34611 | 70000 |
| Quick | 95321 | 42888 | 332909 | 22059 | 215474 | 31191 | 245321 | 27143 |
| Quick2 | 74318 | 56365 | 81282 | 32109 | 81216 | 38250 | 130988 | 33501 |
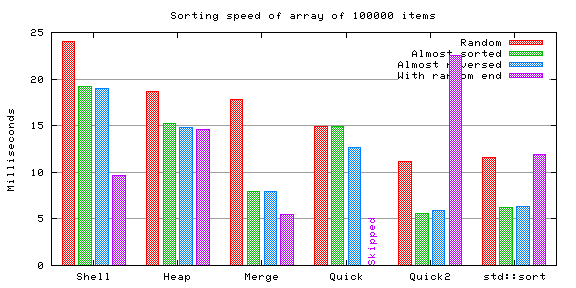
The pathological case for vanilla quicksort was skipped here because the time was several times larger than all the others (and would have rendered the chart almost useless because of the scale difference). For some inexplicable reason the optimized quicksort starts showing problems with this case too (I can't figure out any rational explanation for this).
| Random | Almost sortd | Almost rev. | Random end | |||||
|---|---|---|---|---|---|---|---|---|
| Alg. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. |
| Shell | 3889355 | 4885915 | 2888522 | 3848833 | 2923329 | 3950839 | 1644842 | 2600599 |
| Heap | 3019602 | 4724840 | 3025466 | 4793870 | 2937598 | 4518492 | 3132335 | 70762 |
| Merge | 1566518 | 1800000 | 1464833 | 1800000 | 1463535 | 1800000 | 879336 | 1800000 |
| Quick | 2547886 | 1153959 | 9731476 | 574017 | 5967669 | 849518 | - | - |
| Quick2 | 2023167 | 1432955 | 2153949 | 770245 | 2185309 | 910995 | 2707046 | 554394 |
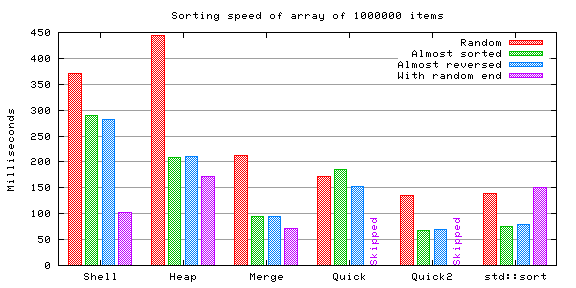
The (unexplicably) pathological case for the optimized quicksort was also skipped here because it was several times larger than any of the others.
| Random | Almost sortd | Almost rev. | Random end | |||||
|---|---|---|---|---|---|---|---|---|
| Alg. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. |
| Shell | 65103669 | 9993926 | 47132297 | 58777435 | 47029110 | 59435171 | 18462731 | 5661000 |
| Heap | 36793778 | 57144949 | 36739278 | 57652356 | 36018473 | 55146281 | 13463210 | 10746174 |
| Merge | 18715987 | 20000000 | 17695109 | 20000000 | 17694108 | 20000000 | 10097147 | 20000000 |
| Quick | 30487732 | 13811163 | 48733767 | 6710516 | 69814521 | 10289213 | - | - |
| Quick2 | 24228590 | 16697372 | 25937307 | 8782867 | 27003925 | 10274957 | - | - |
The performance of the enhanced quicksort compared to the vanilla quicksort becomes clear when comparing the amount of comparisons they perform. Merge sort seems to excel in this category too.
Shell sort and heap sort don't show too much of a difference, even though the former might be slightly slower in average with very big arrays. Almost sorted arrays seem to be faster for both to sort.
Merge sort resulted to be very fast, not losing to its faster competitors. However, part of this speed might be explained in this test because of the slight optimization I used (ie. the function doesn't need to allocate the secondary array each time it is called). Definitely a strong option if the extra memory requirement is not a problem.
Quicksort showed its untrustworthiness. The vanilla version expectedly,
the optimized version quite unexpectedly (I can't figure out why). This
demonstrates that making a good implementation of quicksort is
far from easy. The std::sort function demonstrates that it
is possible, though.
It is interesting to note that the std::sort results
mimic quite faithfully those of the optimized quicksort (which is to
be expected since it uses a similar algorithm). In the pathological
case either an alternative algorithm in the former kicked in, or there might
be some kind of bug in my implementation.
Another interesting detail is that quicksort performs considerably less assignments than comparisons, unlike all the other algorithms. Merge sort performs even better in this category, but makes considerably more assignments (although due to the nature of the algorithm, it consistently makes always the same amount of assignments, which in some cases may be a good thing).