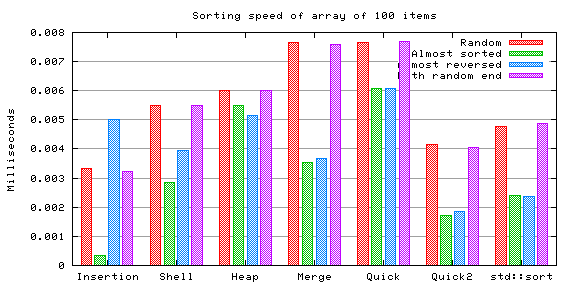
This test is basically the same as the previous one, except that in this case there is a lot of repetition in the data. The data was generated with random values between 0 and 1/100 of the size of the array. This means that each value is repeated, in average, about 100 times. I was interested in knowing if high repetition makes any difference in the sorting algorithms.
In order to see better the difference between the two cases, both charts, ie. the ones in the previous test and this test are shown together (the new chart below the old one).

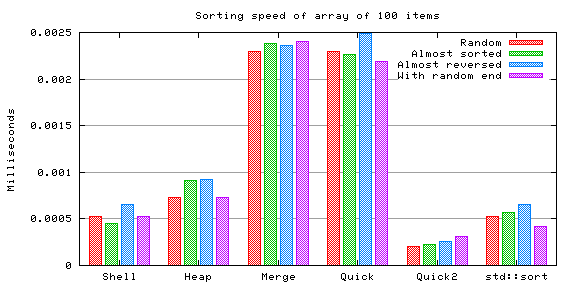
In this case all the items are actually the same (0), so this is a rather special (but interesting) case. The reason why all the bars are not equal for each algorithm is probably due to small inaccuracies at timescales this small (less than 0.5 microseconds).
Insertion sort was skipped because in this case it is trivially enormously faster than the others (linear time).
Having all the items equal seems to cause considerably faster sorting times in all cases (in the previous test the average time was about 4 microseconds, and in this case about 1.5 microseconds).
| Random | Almost sortd | Almost rev. | Random end | |||||
|---|---|---|---|---|---|---|---|---|
| Alg. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. |
| Shell | 282 | 564 | 282 | 564 | 289 | 572 | 282 | 564 |
| Heap | 294 | 297 | 294 | 297 | 294 | 297 | 294 | 297 |
| Merge | 316 | 800 | 316 | 800 | 316 | 800 | 316 | 800 |
| Quick | 830 | 948 | 830 | 948 | 830 | 939 | 830 | 948 |
| Quick2 | 430 | 663 | 430 | 663 | 430 | 660 | 430 | 663 |
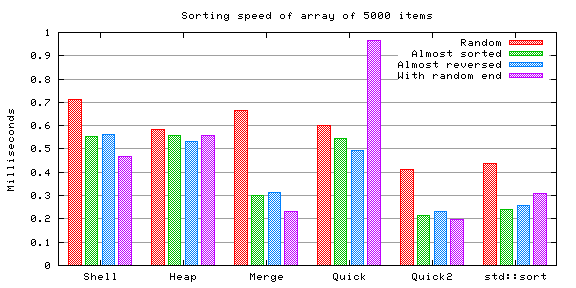
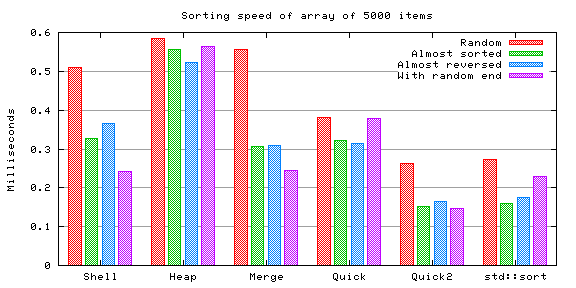
Shell sort is somewhat faster, no difference in heap sort nor in merge sort, and the quicksorts are also somewhat faster. Other than that there's surprisingly little difference.
| Random | Almost sortd | Almost rev. | Random end | |||||
|---|---|---|---|---|---|---|---|---|
| Alg. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. |
| Shell | 69325 | 104376 | 48087 | 81619 | 55616 | 92884 | 42892 | 76284 |
| Heap | 106642 | 168690 | 101201 | 161595 | 102329 | 158034 | 109923 | 176862 |
| Merge | 56557 | 70000 | 52281 | 70000 | 51045 | 70000 | 38744 | 70000 |
| Quick | 82239 | 66783 | 165579 | 50407 | 122510 | 58662 | 307511 | 58991 |
| Quick2 | 56976 | 54584 | 56040 | 37851 | 57104 | 44643 | 92514 | 45010 |
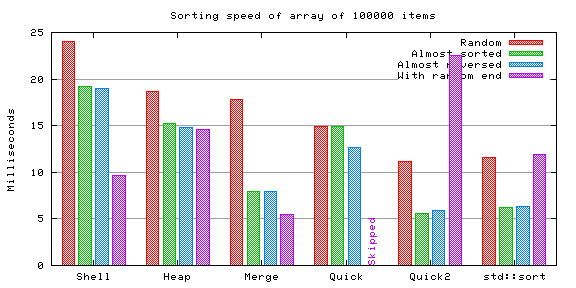
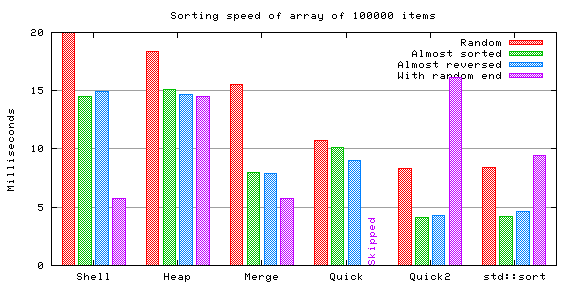
The same trend continues.
| Random | Almost sortd | Almost rev. | Random end | |||||
|---|---|---|---|---|---|---|---|---|
| Alg. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. |
| Shell | 3153522 | 4149856 | 2105087 | 3065171 | 2250156 | 3277592 | 1153748 | 2109500 |
| Heap | 3018543 | 4721747 | 2930637 | 4620850 | 2933508 | 4510015 | 3098751 | 15569 |
| Merge | 1566268 | 1800000 | 1478020 | 1800000 | 1462979 | 1800000 | 965893 | 1800000 |
| Quick | 2296878 | 1631423 | 6685164 | 1096403 | 4180055 | 1393463 | - | - |
| Quick2 | 1674293 | 1398385 | 1608271 | 857867 | 1643649 | 997362 | 2369313 | 889930 |
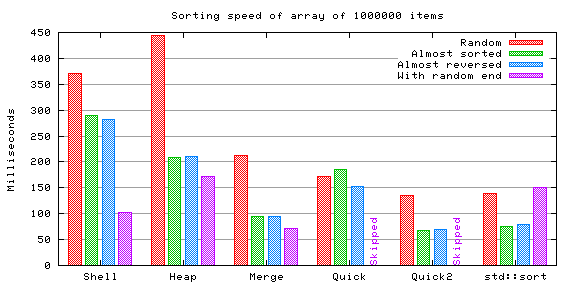
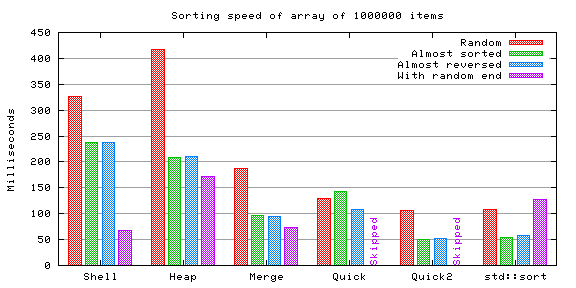
As the size of the array grows, the charts start more and more mimicking each other. Only shell sort seems to benefit from the repetition.
| Random | Almost sortd | Almost rev. | Random end | |||||
|---|---|---|---|---|---|---|---|---|
| Alg. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. | Comp. | Assig. |
| Shell | 57479599 | 2369566 | 37902877 | 49546185 | 39400501 | 51806490 | 13577175 | 913309 |
| Heap | 36792721 | 57141457 | 36294211 | 56833423 | 36006323 | 55119587 | 13249697 | 10399311 |
| Merge | 18715750 | 20000000 | 17826472 | 20000000 | 17693448 | 20000000 | 10965597 | 20000000 |
| Quick | 27966359 | 18585637 | 26793412 | 12089254 | 50881445 | 15805873 | - | - |
| Quick2 | 20900442 | 16328183 | 21561775 | 9718281 | 21619043 | 11154983 | - | - |
Perhaps a bit surprisingly having a lot of repetition in the data doesn't seem to make too much of a difference, especially with larger arrays. Shell sorts seems to benefit in all cases, though.